Sugestão de aulas - Trilha da medida

Esta sugestão de aula foi apresentada na disciplina de Experimentação no Ensino de Ciências da especialização em Ensino de Ciências da Natureza e Educação Matemática, como um relatório com proposta de experimentação no ensino de ciências, abordando uma ou mais das disciplinas Biologia, Física, Matemática e Química.

Introdução e Justificativa

A BNCC destaca suas dez competências gerais e as relaciona a todas as habilidades elencadas para cada uma das séries do ensino básico. A competência 2 (Pensamento científico, crítico e criativo) resume o que acredito encaixar bem para práticas de experimentação em matemática e nisso já se percebe a sua importância no ensino e na aprendizagem.

Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas. (MEC, – BNCC p.9).

Em matemática, as leituras a respeito de experimentação levaram ao entendimento de que ela ocorre em práticas de: a) construções (quando se lida com medidas, com definições e com o uso de materiais concretos), na representação figural aliada a outras representações; b) manipulação de materiais; c) simulações em ambientes digitais; d) na interpretação matemática de experimentos em outras áreas (por exemplo, química e física); e e) na modelagem matemática.

Klein, Dattein e Uhmann (p. 4, 2013) apontam que trabalhar com práticas experimentais tem como vantagem a oportunidade do estudante se sentir envolvido no desenvolvimento das aulas, por permitir-lhes o questionamento e a formulação de hipóteses e possibilitando a construção de sua própria autonomia. Enfatizam ainda sobre o papel de aproximação da percepção cotidiana dos fatos e das coisas aos conceitos científicos apresentados na escola (p. 6).

Ora, práticas de experimentação em matemática são justificadas por sua importância ao instigar o(a) estudante a ser autor de sua própria aprendizagem, no sentido de ser e se perceber parte dos momentos de ensino e de aprendizagem, por oportunizar o desenvolvimento de postura crítica e autônoma.

Objetivos

Observado o DC-GO (Documento Curricular para Goiás) (2018) destacam-se algumas habilidades a respeito de medidas na circunferência e dos números irracionais no 9º ano do ensino fundamental:

• (EF09MA01-A) Compreender que existem problemas, especialmente alguns vinculados à geometria e medidas, cujas soluções não são dadas por números racionais (caso do $\pi$, da $\sqrt{2}$, $\sqrt{3}$, etc.).
• (EF09MA02-C) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica em situações diversas.
• (GO-EF09MA24) Resolver situações-problema envolvendo o cálculo das medidas do comprimento da circunferência e da área do círculo.

Além destas habilidades destacadas, será possível observar a possibilidade de associar outras habilidades e conteúdos da matemática a partir desta proposta de experimento; a título de citação: medidas de tendência central, funções, resolução de situações-problemas, tratamento da informação (gráficos e tabelas), grandezas diretamente e inversamente proporcionais.

Os objetivos da proposta que buscam atender parte destas habilidades são:

• Calcular aproximações para o número $\pi$ a partir de medidas e da relação de duas grandezas: $\frac{C}{d}$ (razão entre o perímetro da circunferência e o seu diâmetro);
• Observar pela proximidade dos resultados que a relação $\frac{C}{d}$ se mantém constante e que esta constante é o número $\pi$;
• Perceber que o número $\pi$ é considerado irracional, pela impossibilidade de se ter para ele uma representação $\frac{a}{b}$, com $a$ e $b$ sendo números inteiros (e $b \neq 0$);
• Compreender como devem ser feitas as medidas das grandezas $C$ e $d$.

Materiais e Métodos

O experimento será desenvolvido em dois espaços: em sala de aula com os estudantes organizados em duplas e no pátio da escola em que cada dupla realizará uma trilha de medidas. O esboço abaixo sugere uma trilha com objetos circulares em que ao passo que se percorre a trilha estes objetos vão ampliando as dimensões (perímetro da circunferência) e (diâmetro da circunferência). A figura abaixo apresenta uma sugestão de organização dos dois espaços e uma sugestão de trilha a ser organizada.

Simulação de organização de espaços: A) Duplas, na sala de aula; B) Trilha de medidas, no pátio.

Os materiais utilizados durante o experimento serão:

• Instrumentos para medida: barbante, régua, fita métrica, trena, metro retrátil etc.;
• Registro de informações: lousa/pincel, computador/notebook, caderno do estudante, planilha eletrônica, projetor;
• Cálculos: caderno, calculadora, planilha eletrônica;

Os métodos e procedimentos utilizados serão:

Momento 1 - Em sala de aula:

• Organização dos estudantes em duplas. É importante trabalhar em dupla por conta da demanda do experimento proposto e para que possa promover uma primeira discussão e decisão entre eles.
• Explicar que cada uma das duplas irá realizar algumas medidas e registrar estas medidas no caderno. Mostrar quais são as duas medidas de grandezas ($C$ e $d$) e dispor suas definições, mas não indicar como os estudantes farão para realizar estas medidas. Observe que existem dois desafios a serem considerados:
• 1) Para alguns objetos a altura em que será medido o perímetro da circunferência ($C$), pois poderão haver decisões diferentes em cada dupla;
• 2) O procedimento feito para encontrar o centro da circunferência, pois nem todos os objetos possuem neles o centro indicado. Esta referência é importante, pois o diâmetro ($d$) é a corda que passa pelo centro da circunferência (O link a seguir é um exemplo de vídeo com procedimento para se encontrar o centro de uma circunferência: https://www.youtube.com/watch?v=bTYXvAIdslc e assim medir seu diâmetro; uma outra forma prática de encontrar o diâmetro pode ser encontrado a distância entre duas retas paralelas entre si e tangentes à circunferência;

Momento 2 - Em sala de aula:

• Orientar os estudantes sobre algumas determinações na trilha:
• Cada dupla deverá escolher três dos sete (ou mais) objetos dispostos na trilha;
• Cada dupla escolherá os instrumentos de medida que utilizará (podendo ser até três instrumentos) e escolherão também os três objetos em que irá realizar as medidas. Na mesa de instrumentos para medida, haverão cartões com os nomes dos objetos, eles deverão pegar três destes cartões e os instrumentos escolhidos;
• O número de cartões com o nome de cada objeto será aproximadamente o mesmo para todos os objetos, de modo que após todas as duplas registrarem as medidas, tenhamos uma quantidade igual de medidas para cada objeto;
• Feito isso, direcionarão para os objetos escolhidos da trilha, realizarão as medidas e voltarão para a sala de aula;
• Todos os estudantes estarão dispostos no pátio. Os que não estiverem na trilha apenas observam e aguardam sua vez de participarem;
• A ordem de participação na trilha será dada por sorteio dos nomes das duplas. Assim que cada dupla realizar a medida num primeiro objeto, será convocada outra dupla para começar a trilha;
• Observe que não foi determinada a forma como as medidas devem ser registradas no caderno ou o que será feito com estas medidas posteriormente. Isto é proposital, para que possam surgir possíveis indagações a respeito do experimento;

Momento 3 - Novamente em sala de aula:

• Observar como foram feitos os registros por cada dupla e explicar que eles não poderão realizar qualquer tipo de alteração nos registros realizados;
• Realizar questionamentos aos estudantes sobre o que fizeram na trilha (estas perguntas são importantes para a continuidade da atividade proposta, para explicar/justificar os resultados do experimento e para consolidar conhecimentos como: medidas e instrumentos de medida, perímetro da circunferência, diâmetro):
• Quais foram os instrumentos escolhidos por cada dupla e por que das escolhas?
• Quais objetos foram escolhidos para medida e por que das escolhas?
• Houve algo desafiante na trilha?
• Que decisões tomaram ao realizar as medidas de perímetro da circunferência e de diâmetro (posição da medida $C$, centro da circunferência)?
• Que relação as duas medidas realizadas em cada objeto os lembra? Espera-se que algum deles possa comentar a respeito das duas medidas, chegando ao passo de citar a fórmula para cálculo do comprimento da circunferência $C= \pi d$ ou $C=2 \pi r$. Este conceito está presente na habilidade EF07MA33 (7º ano) (DC-GO, p. 677): "Estabelecer o número $\pi$ como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica".
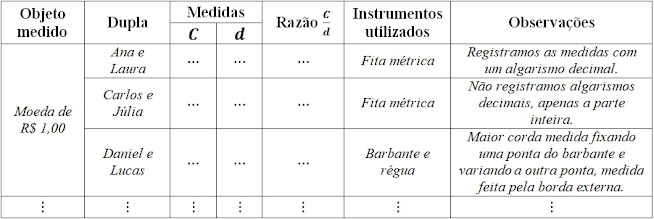
• Registrar na lousa ou em projeção os resultados apresentados por cada uma das duplas. O Quadro abaixo apresenta um exemplo de como organizar os dados coletados nas trilhas e as informações complementares ao experimento;

Exemplo de quadro para registro.

• Tendo registrado as medidas, pedir que cada dupla faça as divisões de $C$ por $d$ e registre na lousa ou repasse os resultados ao(à) professor(a) para inserção no quadro. Registros com dois algarismos na parte decimal (sem arredondamento);
• Retornar a questionar a respeito do que todos percebem sobre os resultados apresentados;
• Quais valores estão mais evidentes por estarem mais próximos uns dos outros?
• Quais valores estão mais distantes? O que vocês acreditam que pode ter ocorrido para estes valores estarem distantes dos demais? Aqui é o momento de discutir sobre os procedimentos utilizados para as medidas e sobre os instrumentos utilizados e como foram utilizados.
• Há uma tendência de que os objetos maiores, quando têm as grandezas medidas adequadamente, retornem valores mais próximos da constante $\pi$. Cabe observar isso nos resultados apresentados pelos estudantes, e argumentar a respeito do porque isso pode ser ocorrido. Maior facilidade no uso do instrumento de medida; minimização do erro dadas as dimensões do objeto medido.
• Caso algum estudante tenha ou não percebido a aproximação das razões ao valor de $\pi$ é momento de:
• Apresentar a fórmula que relaciona a constante;
• Apresentar a constante $\pi$ com alguns algarismos decimais;
• Caso esteja utilizando registros pelo computador/notebook em planilha, criar um gráfico de dispersão XY e adicionar a linha de tendência com função linear aos valores observados pelos estudantes. A figura abaixo mostra uma simulação com dados fictícios sobre o gráfico e linha de tendência, mencionados.

Simulação de gráfico de dispersão XY e linha de tendência (valores fictícios).

• Argumentar sobre a irracionalidade de $\pi$, por meio da definição de números racionais. Aproveitar para relembrar sobre o conjunto dos números reais (racionais e irracionais);
• Enfatizar que a razão $\frac{C}{d}$ não terá ambos os valores $C$ e $d$ como inteiros, sendo que ao menos um deles não será um número inteiro e por isso não se enquadra na definição de número racional;
• Argumentar sobre a presença de números irracionais, como o $\pi$, aplicados a situações reais.

Momento 4 - Novamente na trilha de medidas:

• Cada dupla retornará à trilha, escolhendo um dos objetos medidos e irá refazer as medidas das duas grandezas. Sugere-se que a escolha seja pelo objeto cuja razão $\frac{C}{d}$ ficou mais distante da maioria das outras;
• Neste momento o(a) professor(a) irá orientar a respeito de como deve ser feita a medida procurando minimizar erros e melhorar a aproximação do valor do número $\pi$;
• As duplas que forem revisitar o mesmo objeto já ficarão próximas para que o(a) professor(a) não necessite realizar o mesmo argumento repetidamente. Todos os outros estudantes devem observar também as orientações do(a) professor(a). Os argumentos serão, por exemplo:
• Escolha mais adequada de instrumentos de medida;
• Atenção no momento de medição;
• Posicionamento do instrumento de medida no objeto em relação às grandezas que se quis medir (e aqui reforçar as definições das duas grandezas medidas);
• Procedimento para se encontrar o centro da circunferência;
• Procedimento para se medir o diâmetro de uma circunferência sem passar, necessariamente pelo seu centro (retas paralelas entre si e tangentes à circunferência);
• Questionar e posteriormente argumentar sobre o fato de termos trabalhado com diferentes áreas da matemática (objetos geométricos, medidas, cálculo de divisão com aproximação de um valor, gráfico, tabela etc.);
• Repontuar/revisitar tudo o que foi estudado com o experimento por meio de questionamentos e afirmações.

Resultados Esperados

Acredita-se que serão observados resultados tais como os elencados abaixo:

• Não haverá dificuldade no desenvolvimento do experimento por conta da disponibilidade dos estudantes em participar das atividades propostas;
• Dificuldade no início do experimento em utilizar instrumentos de medidas;
• Dificuldade no início do experimento em saber onde realizar as medidas das duas grandezas (o que é irrelevante para os objetivos do experimento, observando que as duas grandezas sejam medidas num mesmo posicionamento);
• Questionamento sobre como organizar as medidas coletadas no caderno (o(a) professor(a) não deve inferir a este respeito, retornando apenas que se organize conforme a dupla melhor acreditar que deve ser);
• Percepção de que perímetro da circunferência é o mesmo que comprimento da circunferência;
• Haverá percepção de relação entre diferentes áreas na matemática (números, álgebra, geometria);
• Percepção de que os números estão presentes em praticamente tudo que nos cerca e de que eles não necessitam ser exatos (na verdade não há exatidão de números e medidas em nada material);
• Relembrar ou conhecer conceitos de objetos da matemática que deveriam ser estudados em séries anteriores;
• Aprender quanto ao uso adequado dos instrumentos de medida, de que eles não são exatos e que mesmo com toda precisão de atenção e escala dos instrumentos ainda existirá erro de aproximação;
• Oportunidade de utilizar o experimento para tratar da continuidade das habilidades elencadas para esta proposta e de outras habilidades que podem ser associadas a partir deste experimento.

Referências Bibliográficas

KLEIN, Cláudia Luciani; DATTEIN, Raquel Weyh; UHMANN, Rosângela Inês Matos. Um estudo sobre a experimentação no ensino de ciências na formação de professores. VI ENCONTRO REGIONAL SUL DE ENSINO DE BIOLOGIA. p. 1-12, maio 2013.

Ministério da Educação. Base Nacional Comum Curricular. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em 15 dez. 2020.

Secretaria de Estado da Educação (SEDUC). DC-GO – Documento Curricular para Goiás. 2018. Disponível em: https://cee.go.gov.br/wp-content/uploads/2019/08/Documento-Curricular-para-Goi%C3%A1s.pdf. Acesso em 15 dez. 2020.