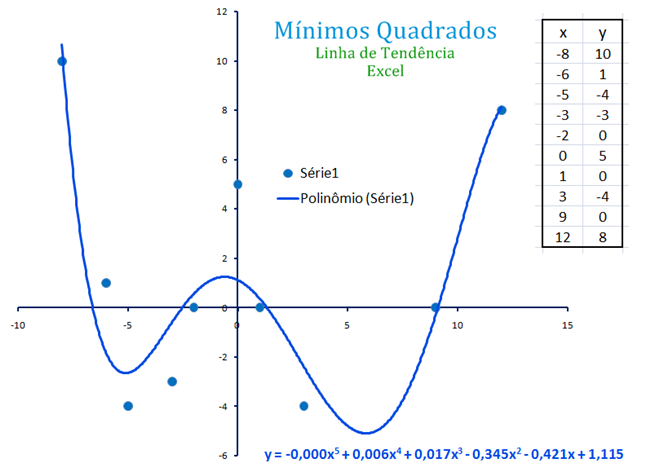
Mínimos quadrados e a linha de tendências em planilhas eletrônicas

Mínimos Quadrados

Um problema comum no trabalho experimental é obter uma relação matemática $y=f(x)$  entre duas variáveis $x$ e $y$ através do ‘ajuste’ de uma curva aos pontos no plano que correspondem aos vários valores de $x$ e $y$ determinados experimentalmente, digamos $(x_1, y_1), (x_2, y_2),\cdots , (x_n, y_n)$.

Na base de considerações teóricas ou simplesmente pelo padrão apresentado pelos pontos, é possível decidir a forma geral da curva a ser ajustada. Algumas possibilidades são as apresentadas na figura acima.

• uma reta: $y=a+bx$
• um polinômio quadrático: $y=a+bx+cx^2$
• um polinômio cúbico: $y=a+bx+cx^2+dx^3$

Como os pontos são obtidos experimentalmente, geralmente há certo “erro” de medição nos dados, tornando impossível encontrar uma curva da forma desejada que passe por todos os pontos. Assim, a ideia é escolher a curva (determinando seus coeficientes) que melhor ajusta os dados.

Ajuste linear de Mínimos Quadrados

Para realizar o ajuste linear $(y = a + bx)$ de mínimos quadrados aos pontos $(x_1, y_1), (x_2, y_2),\cdots , (x_n, y_n)$, é possível escrever $n$  equações de modo a representá-las de forma matricial:

$\begin{bmatrix} 1 & { x }_{ 1 } \\ 1 & { x }_{ 2 } \\ \vdots  & \vdots  \\ 1 & { x }_{ n } \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix}=\begin{bmatrix} { y }_{ 1 } \\ { y }_{ 2 } \\ \vdots  \\ { y }_{ n } \end{bmatrix}$ ou de forma compacta $Av=y$ em que

$A=\begin{bmatrix} 1 & { x }_{ 1 } \\ 1 & { x }_{ 2 } \\ \vdots  & \vdots  \\ 1 & { x }_{ n } \end{bmatrix}$   $v=\begin{bmatrix} a \\ b \end{bmatrix}$  e   $y=\begin{bmatrix} { y }_{ 1 } \\ { y }_{ 2 } \\ \vdots  \\ { y }_{ n } \end{bmatrix}$

Se os pontos forem colineares é facilmente possível encontrar a reta que neste caso, passaria por todos os pontos, e assim os coeficientes e seriam conhecidos.

Comumente, os pontos não são colineares, o que torna impossível encontrar os coeficientes de modo a satisfazer as equações. Para casos assim, procuramos encontrar uma solução de mínimos quadrados.

As distâncias percebidas dos pontos à reta indicam uma medida do “erro” que resulta num determinado ponto do ajuste inexato de $y=a_*+b_*x$ a este ponto de dados.

Teorema. Seja $(x_1, y_1), (x_2, y_2),\cdots , (x_n, y_n)$ um conjunto de dois ou mais pontos de dados, não todos em uma reta vertical, e sejam:

$A=\begin{bmatrix} 1 & { x }_{ 1 } \\ 1 & { x }_{ 2 } \\ \vdots & \vdots \\ 1 & { x }_{ n } \end{bmatrix}$ e $y=\begin{bmatrix} { y }_{ 1 } \\ { y }_{ 2 } \\ \vdots \\ { y }_{ n } \end{bmatrix}$

Então, existe um único ajuste linear de mínimos quadrados $y=a_*+b_*x$ aos pontos de dados. Além disso, $v_*=\begin{bmatrix} a_* \\ b_* \end{bmatrix}$ é dado por $v_*=(A^T  \cdot A)^{-1}\cdot A^T\cdot y$ que expressa a unicidade da solução da equação normal.

Exemplo:

Encontre o ajuste linear de mínimos quadrados aos quatro pontos $(0, 1), (1, 3), (2, 4) $ e $( 3, 4)$.
Tem-se $A=\begin{bmatrix} 1 & 0 \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \end{bmatrix}$, $A^T\cdot A=\begin{bmatrix} 4 & 6 \\ 6 & 14 \end{bmatrix}$ e $(A^T\cdot A)^{-1}=\dfrac{1}{10}\begin{bmatrix} 7 & -3 \\ -3 & 2 \end{bmatrix}$

Como $v_*=(A^T  \cdot A)^{-1}\cdot A^T\cdot y$, segue
$v_*= \dfrac{1}{10}\begin{bmatrix} 7 & -3 \\ -3 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 2 & 3 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 3 \\ 4 \\ 4 \end{bmatrix} = \begin{bmatrix} 1,5 \\ 1 \end{bmatrix}$ e assim a reta desejada é $y = 1,5 + x$.

Resolver problemas usando este método tem se mostrado mais simples quando usamos a equação $A^T \cdot A \cdot v = A^T \cdot y$; tornando o procedimento um pouco diferente de quando usamos a forma $v_*=(A^T  \cdot A)^{-1}\cdot A^T\cdot y$.

Do modo sugerido, $A^T \cdot A \cdot v = A^T \cdot y$ após fazer as substituições devidas e realizar as multiplicações entre as matrizes, chega-se em um sistema, resolvendo o sistema teremos o resultado esperado para $v$. Assim, não realizamos o cálculo para encontrar a matriz inversa.

Ajuste Polinomial de Mínimos Quadrados

A técnica descrita para ajustar uma reta de mínimos quadrados pode facilmente ser generalizada para ajustar um polinômio de qualquer grau especificado a pontos de dados.

$A=\begin{bmatrix} 1 & { x }_{ 1 } & { x }_{ 1 }^{ 2 } & \cdots  & { x }_{ 1 }^{ m } \\ 1 & { x }_{ 2 } & { x }_{ 2 }^{ 2 } & \cdots  & { x }_{ 2 }^{ m } \\ \vdots  & \vdots  & \vdots  & \cdots  & \vdots  \\ 1 & { x }_{ n } & { x }_{ n }^{ 2 } & \cdots  & { x }_{ n }^{ m } \end{bmatrix}$,   $y=\begin{bmatrix} { y }_{ 1 } \\ { y }_{ 2 } \\ \vdots  \\ { y }_{ n } \end{bmatrix}$   e   $v=\begin{bmatrix} { a }_{ 0 } \\ { a }_{ 1 } \\ \vdots  \\ { a }_{ m } \end{bmatrix}$.

Analogamente ao ajuste linear, teremos as soluções das equações normais $A^T \cdot A \cdot v = A^T \cdot y$ determinando os coeficientes dos polinômios ou de modo a visualizar a única solução, dada por $v_*=(A^T  \cdot A)^{-1}\cdot A^T\cdot y$.

Confira complementos deste conteúdo no material disponível para download.

Linha de tendências no Excel

Nas planilhas eletrônicas, em específico neste caso ao Excel, há uma forma simples de observar o ajuste feito pelo método dos mínimos quadrados, que é o uso da linha de tendências em gráficos de dispersão XY. Confira os passos para chegar ao resultado:

• [1] Em duas colunas adicione as coordenadas $(x, y)$ dos pontos em que se deseja realizar o ajuste;
• [2] Clique em Inserir;
• [3] Clique em Dispersão;
• [4] Clique no primeiro item (Dispersão Somente com Marcadores);

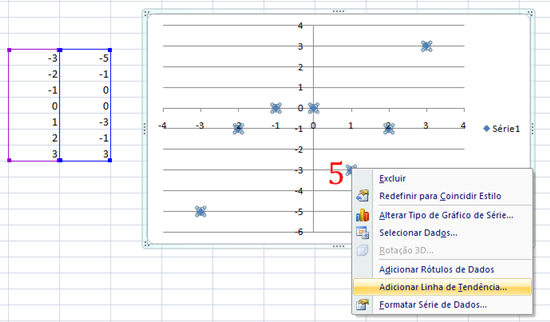
• [5] Clique-direito sobre um dos pontos do gráfico e em seguida clique em Adicionar Linha de Tendência...

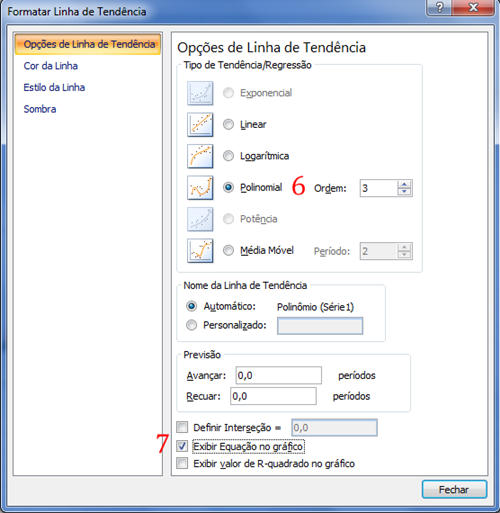
• [6] Na janela que aparece, escolha o tipo de tendência (neste caso, foi escolhido um polinômio de 3º grau);
• [7] Clique-selecione o item Exibir Equação no gráfico.

• Clique em Fechar e confira o resultado;

Neste exemplo, utilizamos os pontos $(-3, -5)$, $(-2, -1)$, $(-1, 0)$, $(0, 0)$, $(1, -3)$, $(2, -1)$, $(3, 3)$ e o ajuste cúbico resultante foi $f(x)=0,305x^2-0,011x^2-1,388x-0,952$.

Material complementar sobre Mínimos Quadrados

Seguem alguns materiais que complementam esta postagem. Nele consta o texto completo deste conteúdo, alguns exemplos adicionais e planilhas com gráficos destes e outros exemplos. Os arquivos (conteúdo complementar em .pdf e planilhas em Excel .xlsx) estão compactados no formato .rar.

Material Complementar [Google Drive]
Material Complementar [Box]