Nesta postagem você confere uma coleção de atividades e conteúdos da matemática que envolvem ângulos. Estas atividades estão organizadas conforme expectativas de aprendizagem que estão indicadas no Documento Curricular de Goiás (DC-GO).
Download
Você poderá acessar todo o material que está descrito mais abaixo através dos links que seguem. Estão disponíveis dois arquivos do mesmo material, um em versão .doc para edição e outro em .pdf para manter a formatação original. As duas versões estão com cabeçalho de uma das escolas em que trabalho.
Expectativa de aprendizagem: Reconhecer a abertura do ângulo como grandeza associada às figuras geométricas.
Ângulos
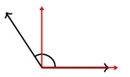
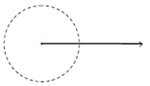
As imagens abaixo indicam representações concretas de ângulos.
Ângulo é a figura geométrica formada por duas semirretas de mesma origem. É a região entre estas duas semirretas.
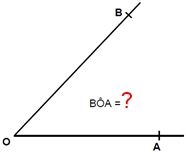
As semirretas $\overrightarrow {OA}$ e $\overrightarrow {OB}$ são lados do ângulo. O ponto $O$ é o vértice do ângulo. Indicamos este ângulo por $A\hat{O}B$, $B\hat{O}A$ ou, apenas, $\hat{O}$.
Tarefa
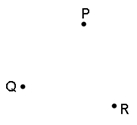
1. Observe os pontos $P$, $Q$ e $R$ abaixo.
Trace o ângulo de vértice $P$ e lados formados pelas semirretas $\overrightarrow {PQ}$ e $\overrightarrow {PR}$. Indique esse ângulo de três formas diferentes: _____, _____e ____.
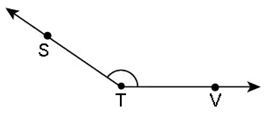
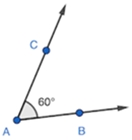
2. Considere o ângulo abaixo:
a) Como ele pode ser indicado? _____, _____e ____.
b) Qual é o vértice desse ângulo? ______.
c) Quais são os lados? ______ e ______.
3. Pesquise em jornais e/ou revistas, imagens que dão ideia de ângulo. Recorte-as, marque as partes que lembram ângulo e cole abaixo.
Expectativas de aprendizagem: Associar mudanças de direção e giros em trajetos em malhas quadriculadas e da leitura de mapas à noção e uso do ângulo em situações diversas. Resolver problemas que envolvam a noção de ângulo em diferentes contextos e em situações reais, como ângulo de visão. Identificar ângulos formados nas plantas baixas. Identificar ângulos: nulo, reto, raso, meia volta e de uma volta.
Giros e Ângulos
Os babilônios foram uma civilização antiga que viveram Mesopotâmia (atualmente onde fica o Iraque) por volta de 1.700 a.C. Eles usavam um sistema de numeração de base de 60 e acreditavam que o Sol girava em torno da Terra, em uma órbita com a forma de circunferência, e que esse giro durava 360 dias, ou seja, 1 ano equivalia a 360 dias.
O sábio grego Hiparco de Niceia, que viveu por volta de 180 a.C. a 125 a.C., provavelmente influenciado pelos conhecimentos dos babilônios, dividiu a circunferência em 360 partes iguais, criando a unidade de medida de abertura de ângulos (e arcos) chamada grau, que é simbolizado por $^\circ$.
Com isso, cada parte das 360 partes de uma circunferência é igual a 1 grau e é indicada por $1^\circ$. E a volta toda da circunferência mede $360^\circ$.
Tarefa
1. Siga as instruções:
a) Nomeie o ponto inicial de $A$.
b) A partir do ponto $A$ e orientado pela seta, siga 3 quadros para frente.
c) Gire um quarto de volta para o sentido horário e siga 5 quadros para frente.
d) Gire três quartos de volta no sentido horário e siga 8 quadros para frente.
e) Gire meia volta no sentido horário e siga 2 quadro para frente.
f) Gire um quarto de volta no sentido anti-horário e siga 2 quadros para frente.
g) Marque o ponto $B$ na posição em que se encontra.
2. Observe a imagem abaixo:
Saindo da casa de Carla e fazendo o trajeto indicado na imagem, quantas meias voltas são feitas para chegar à casa de Maria?
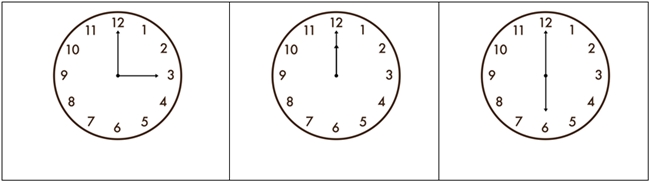
3. Indique nos relógios abaixo, os giros entre os ponteiros (são dois giros: sentido horário e sentido anti-horário):
4. O ângulo de visão altera a qualidade da imagem dependendo de qual posicionamento você se encontra em relação à TV. A TV de plasma é a que melhor apresenta um ângulo de visão que chega a meia volta ($180^\circ$) sem perda de qualidade. A pessoa da imagem abaixo está assistindo a uma TV que permite um ângulo de visão de um quarto de volta ($90^\circ$), ou seja, em três quartos de volta ($270^\circ$) a pessoa não terá ângulo de visão na TV. Na imagem abaixo é possível perceber o ângulo de visão de quem está assistindo à TV.
a) Qual é o nome do ângulo de meia volta?
b) Qual é o nome do ângulo de um quarto de volta?
5. Nos relógios abaixo, desenhe o ponteiro de modo a obter os giros pedidos (não se importe com a hora correta, um dos ponteiros deverá estar sempre apontando para o 12):
Expectativas de aprendizagem: Reconhecer e comparar ângulos. Reconhecer os diferentes tipos de ângulos: agudo, reto e obtuso. Classificar ângulos em agudo, reto, obtuso.
Tipos de Ângulos
Um ângulo reto é um ângulo de medida igual a $90^\circ$. Um ângulo reto tem a forma e um canto quase perfeito, como o canto de uma folha de papel retangular ou o canto de encontro de duas paredes de uma sala reta.
Um ângulo agudo é um ângulo cuja medida em graus é menor do que $90^\circ$.
Um ângulo é obtuso quando suam medida em graus é maior que $90^\circ$ e menor que $180^\circ$.
Um ângulo retraente ou côncavo é um ângulo com medida maior que $180^\circ$ e menor que $360°^\circ$.
1. Corresponda:
3. Adicione nomes aos vértices que formam os ângulos na questão anterior e indique cada um dos ângulos dentro de cada retângulo.
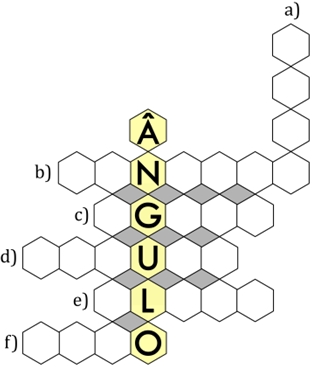
4. Complete a colméia dos ângulos e escreva a característica de cada um:
Expectativa de aprendizagem: Identificar ângulos congruentes, complementares e suplementares.
Ângulos congruentes, complementares, suplementares e adjacentes
Dois ou mais ângulos são considerados congruentes quando possuem a mesma medida. Os ângulos $B\hat{A}C$ e $E\hat{D}F$ são congruentes.
Dois ângulos são complementares quando a soma entre eles é igual a $90^\circ$ (ângulo reto).
Dois ângulos são suplementares quando a soma entre eles é igual a $180^\circ$ (ângulo raso).
Dois ângulos são adjacentes quando compartilha um dos lados, ou seja, quando possuem um lado em comum.
Tarefa
1. Complete, classificando os pares de ângulos adjacentes abaixo:
2. Observe os pares de ângulos. O que eles são um em relação ao outro em cada par?
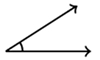
3. Use uma régua e desenhe o ângulo complementar ao ângulo abaixo:
Expectativa de aprendizagem: Determinar medidas da abertura de ângulos, por meio de transferidor e/ou tecnologias digitais, associando a situações reais como ângulos de visão, dentre outros.
O transferidor
O instrumento usado para medir aberturas de qualquer ângulo, em graus, é o transferidor.
Centro do transferidor: ponto médio da linha de fé.
Limbo: região do transferidor que contem a graduação dos ângulos.
Como medir?
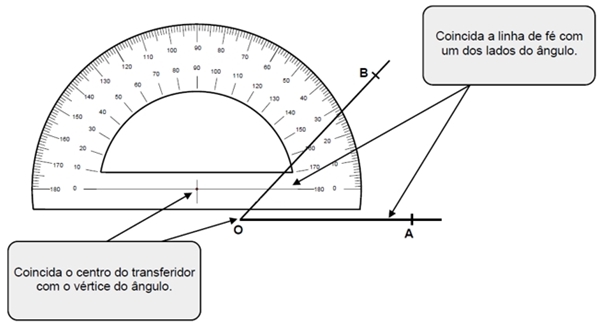
- Coloque o transferidor sobre o ângulo, fazendo coincidir o centro do instrumento com o vértice do ângulo e, a linha de fé, com um dos lados do ângulo.
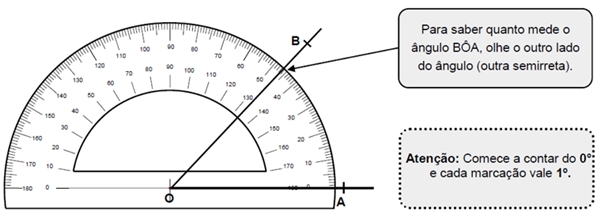
- Iniciando a contagem sempre do zero, verifique o número da graduação que se encontra no outro lado do ângulo. O valor indicado é a medida do ângulo.
- Se achar necessário, prolongue os lados com a régua.
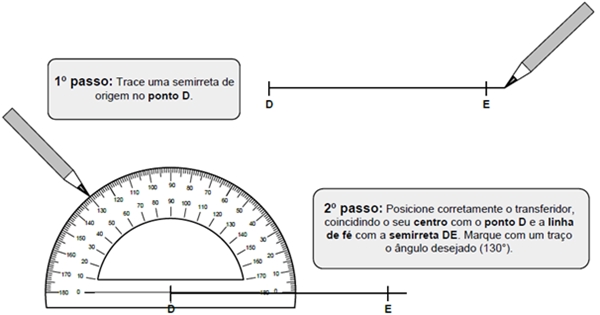
Como construir um ângulo?
1. Agora é com você! Construa um ãngulo com a medida de $70^\circ$.
2. Escreva a medida dos ângulos indicados abaixo, observando a imagem:
3. Meça os ângulos e indique as medidas:
Tarefa
Meça os ângulos abaixo:
Referências
Apostila Ângulos. Disponível em: http://www.cp2.g12.br/blog/re2desenho/files/2019/10/5-Capitulo_IV-6o-Ano-GABARITO2.pdf, acesso em 8 jul. 2022.
BRASIL/MEC. BNCC - Base Nacional Comum Curricular. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf, acesso: 8 jul. 2022.
Este material é fruto de algumas referências coletadas na web, com edições em material já disponível e outras propostas novas.
Algumas referências não foram lembradas quando da disponibilização deste material aqui na web. Assim que formos as identificando atualizaremos as referências.
As referências abaixo não foram utilizadas neste material, mas são ótimos materiais complementares:
Comente este artigo: