Exercício de matemática sobre proporção entre áreas

Exercício de matemática sobre decomposição de áreas de polígonos regulares

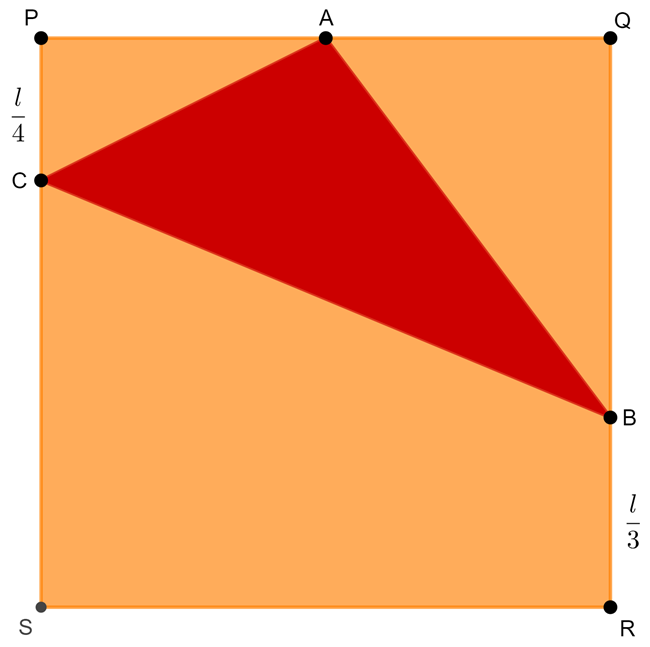
Observe na imagem abaixo a composição de duas regiões poligonais um quadrado de lado $l$ e um triângulo com vértices sobre lados do quadrado, tendo que o ponto $A$ é ponto médio do segmento $PQ$. Qual é a razão entre a área do triângulo e a área do quadrado?

Proposta de solução

Observe que temos duas informações importantes na representação das regiões, a medida do segmento $CP$ valendo $\cfrac{l}{4}$ e a medida do segmento $BR$ valendo $\cfrac{l}{3}$, temos ainda que $A$ é ponto médio do segmento $PQ$. A partir destas informações e tendo que o lado do quadrado é dado pela medida $l$ (lados: $SR$, $QR$, $PS$ e $PQ$) construímos outra imagem com informações complementares e subdivisões de áreas que servirão para os cálculos de áreas do quadrado e do triângulo $\triangle ABC$.

Observe que na nova construção, foram realizadas divisões das subáreas $A_1$, $A_2$, $A_3$, $A_4$ e $A_5$ o triângulo em azul. As áreas $A_1$, $A_2$, $A_3$ e $A_5$ são triangulares e $A_4$ é um retângulo. Na construção foram complementadas as medidas dos segmentos que formam os lados de cada um das sub-regiões. Vamos aos cálculos das áreas e junto explicações sobre como chegamos às medidas dos lados.

Cálculo da área do quadrado $PQRS$

A área de uma região poligonal retangular (quadrado) é dada por $A = l^2$. Como o lado do quadrado $PQRS$ é $l$, temos que:

$A_{quadrado} = l^2$.

Cálculo da área $A_1$

A área da região triangular é dada por $A = \cfrac{b \cdot h}{2}$. O triângulo de área $A_1$ é $\triangle ACP$, cujos lados medem $b = \frac{l}{2}$ e $h= \frac{l}{4}$. Temos que:

$A_1 = \cfrac{\frac{l}{2} \cdot \frac{l}{4}}{2} = \cfrac{\frac{l^2}{8}}{2} = \cfrac{l^2}{16}$

Cálculo da área $A_2$

O triângulo de área $A_2$ é $\triangle ABQ$, cujos lados medem $b = \frac{l}{2}$ e $h= \frac{2l}{3}$. Temos que:

$A_2 = \cfrac{\frac{l}{2} \cdot \frac{2l}{3}}{2} = \cfrac{\frac{l^2}{3}}{2} = \cfrac{l^2}{6}$

Cálculo da área $A_3$

O triângulo de área $A_3$ é $\triangle BCD$, cujos lados medem $b = l$ e $h= \frac{5l}{12}$. Temos que:

$A_3 = \cfrac{l \cdot \frac{5l}{12}}{2} = \cfrac{\frac{5l^2}{12}}{2} = \cfrac{5l^2}{24}$

Cálculo da área $A_4$

A área de uma região poligonal retangular é dada por $A = c \cdot l$ ($c$ é comprimento e $l$ é largura, usado aqui como L para não confundir com a medida do lado do quadrado). Então o retângulo $BDSR$ de lados $c = l$ e $L = \frac{l}{3}$ tem como área $A_4$ dada por:

$A_4 =  l \cdot \cfrac{l}{3}= \cfrac{l^2}{3}$

Cálculo da área $A_5$

A área do triângulo $\triangle ABC$ é dada por:

$A_5=A_{quadrado} - (A_1 + A_2 + A_3 + A_4)$

$A_5= l^2 - \left(\cfrac{l^2}{16}+\cfrac{l^2}{6}+\cfrac{5l^2}{24}+\cfrac{l^2}{3} \right)$

$A_5= l^2 - \left(\cfrac{3l^2 + 8l^2 + 10l^2 + 16l^2}{48} \right)$

$A_5= \cfrac{48l^2 - 37l^2}{48}$

$A_5= \cfrac{11l^2}{48}$

Razão entre a área do triângulo $\triangle ABC$ e do quadrado $PQRS$

Observe que a razão entre a área do triângulo $\triangle ABC$ e do quadrado $PQRS$ é dada por $\cfrac{A_5}{A_{quadrado}}$, então temos:

$\cfrac{A_5}{A_{quadrado}} = \cfrac{\frac{11l^2}{48}}{l^2} = \cfrac{11l^2}{48l^2}= \cfrac{11}{48}$

Portanto, a razão entre a área do triângulo $\triangle ABC$ e do quadrado $PQRS$ é $\cfrac{11}{48}$.