Uma característica importante na matemática é a percepção de recorrências, de características comuns, de padrões. Isso permite formular regras [cuidado com as generalizações] que encurtam cálculos, que com a prática, após um tempo se tornam comuns e isso provoca agilidade e percepção mais apurada de caminhos para, por exemplo, resolver situações-problemas, ou seja, interpretar e propor possíveis soluções torna-se mais simples.
Este post foi criado por recomendação do leitor Pedro Rafael Neto.
É preciso tomar cuidado e compreender bem os procedimentos e em que situações eles se aplicam ou regras que encurtam cálculos básicos podem acabar provocando uma série de erros [cuidado com a teorização a todo custo]. É Pedro você acabou contribuindo na verdade para que eu criasse dois posts. Aqui veremos algumas regrinhas, no próximo veremos sobre o que é realmente importante para a Aprendizagem em Matemática. Os professores não costumam ensinar algumas dessas regras, por exemplo a percepção da sequência na multiplicação, justamente porque elas não passam de DECOREBAS, e se não compreendido o procedimento, elas não contribuem para o aprendizado.
Regra para a tabuada de multiplicação por 6, 7, 8 e 9
As regras a seguir são válidas para as tabuadas de $6$ a $9$, multiplicadas por $5$, $6$, $7$, $8$ ou $9$. O procedimento é o seguinte (usaremos $6 \cdot 8$ para exemplificar):
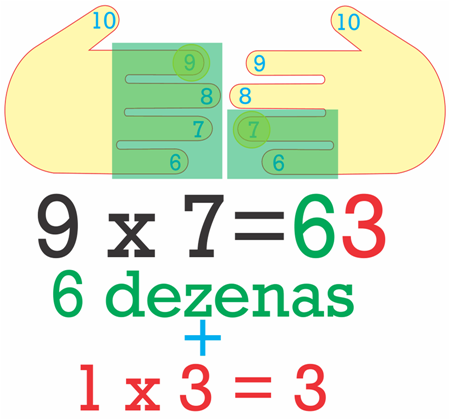
# Coloque as mãos na configuração da figura e memorize a numeração dos dedos das duas mãos de baixo para cima de $6$ a $10$:
# Na mão esquerda destaque os dedos do primeiro fator (multiplicando) e na mão direita destaque os dedos do segundo fator (multiplicador):
# Some o número de dedos destacados e multiplique por $10$:
$4 \cdot 10 = 40$.
# Multiplique o número de dedos da mão esquerda pelo número de dedos da mão direita:
$4 \cdot 2 = 8$.
# Some os dois resultados:
$40 + 8 = 48$.
# $48$ é o resultado de $6 \cdot 8$. Pronto!
Observe as configurações das mãos e verifique com outros valores:

A carreirinha nada mais é que a observação feita por crianças quando começam a estudar multiplicação usando a tabuada. Elas logo percebem o padrão nos resultados da multiplicação.
Veja uma assimilação:
# nestes cálculos tomemos a forma $p \cdot q = ab$.
$q -1 = a$
$p - a = b$
Para realizar a multiplicação da tabuada de $9$ usando as suas mãos basta:
$15 \cdot 100 = 1.500$
$9 \cdot 1.000 = 9.000$
$0,005 \cdot 100 = 0,5$
$\cfrac {3,7} {100} = 0,037$
# a "vírgula caminhara para traz".
Você conseguiu compreender? Faça o teste para outros quadrados e confira!
[2] Contar (Matemática.com).
Observe as configurações das mãos e verifique com outros valores:
"Contando nas mãos [6 vezes]"
"Contando nas mãos [7 vezes]"
"Contando nas mãos [8 vezes]"
"Contando nas mãos [9 vezes]"
Regras para a tabuada de multiplicação por 9
"Carreirinha"

A carreirinha nada mais é que a observação feita por crianças quando começam a estudar multiplicação usando a tabuada. Elas logo percebem o padrão nos resultados da multiplicação.
Na primeira coluna as dezenas dos resultados das multiplicações crescem de $0$ a $9$; na segunda coluna as unidades dos resultados das multiplicações decrescem de $9$ a $0$.
Veja uma assimilação:
# nestes cálculos tomemos a forma $p \cdot q = ab$.
$q -1 = a$
$p - a = b$
"Contando nas mãos"
Para realizar a multiplicação da tabuada de $9$ usando as suas mãos basta:
- contar da esquerda para a direita os dedos, de $1$ a $10$ conforme a figura;
- abaixar o dedo que possui o mesmo número em ordem, da multiplicação por $9$ desejada;
- os dedos que estiverem à esquerda do dedo abaixado, são as dezenas;
- os dedos que estiverem à direita do dedo abaixado, são as unidades.
Decompondo e multiplicando
Um conteúdo aprendido ainda no ensino fundamental (fase 1) que é pouco utilizado e que colabora para o raciocínio rápido é realizar cálculos com auxílio da decomposição (ele pode ser utilizado nas operações básicas e com um pouco de prática, você irá conseguir realizar cálculos com mais facilidade). Confira os exemplos de cálculos com decomposição em multiplicação:
$263 \cdot 2 = 200 \cdot 2 + 60 \cdot 2 + 3 \cdot 2 = 400 + 120 + 6 = 526$.
$359 \cdot 27 = (300 \cdot 2 + 50 \cdot 2 + 9 \cdot 2) \cdot 10 + (300 \cdot 7 + 50 \cdot 7 + 9 \cdot 7) =$
$= (600 + 100 + 18) \cdot 10 + (2.100 + 350 + 63)$
$= 7.180 + 2.513$
$= 9.693$
Multiplicar e Dividir por 10, 100, 1.000, ...
Multiplicando
Quando multiplicamos um número racional por $10, 100, 1000, ...$ (múltiplos de $10$, potências de $10$) é possível perceber já de criança o "acrescentar zeros, tantos quantos existirem no multiplicador". Isso é verdade!
Há uma sugestão de aula na revista Nova Escola, em que alunos do 3º ano (2ª série), utilizam a calculadora para multiplicarem alguns números naturais por $10$, por $100$ e por $1.000$ e fazerem isso algumas vezes. Depois eles são questionados se não perceberam nada. Eles percebem que todos os números multiplicados terminam em zero. Alguns percebem que a quantidade de zeros é a mesma do multiplicando e aí vem a percepção da regularidade. Essa percepção é um encurtamento de cálculo interessante.
$6 \cdot 10 = 60$$15 \cdot 100 = 1.500$
$9 \cdot 1.000 = 9.000$
Mais a frente os alunos aprendem que essa regularidade se estende aos números racionais (incluindo os negativos e os números com vírgula) e percebem uma outra regularidade, em números com vírgula, ao multiplicar, a vírgula caminha para frente, tantas casas quantos zeros existirem no multiplicador $(10, 100, 1000,...)$. E aí é preciso só tomar cuidado para a escrita matemática "vírgula caminhar?" e para a compreensão de que esse caminhar é uma multiplicação por potências de $10$.
$3,49 \cdot 10 = 34,9$$0,005 \cdot 100 = 0,5$
Dividindo
Na divisão a regularidade percebida é a mesma. Observe:
# com números naturais retiram-se zeros do multiplicador, tantos quantos forem os do multiplicando;
$\cfrac{8.000} {10} = 800$
$\cfrac{500} {100} = 5$
# se os zeros a serem retirados no multiplicador não são suficientes, a vírgula surge nos outros algarismos;
$\cfrac{8.400}{1.000} = 8,4$
$\cfrac{495}{10} = 49,5$
# se mesmo assim os algarismos não são suficientes, começam a surgir zeros à esquerda;
$\cfrac {372} {1.000} = 0,372$
$\cfrac {81} {1.000} = 0,081$$\cfrac {3,7} {100} = 0,037$
# a "vírgula caminhara para traz".
Muito cuidado com essas regrinhas! É preciso compreender os procedimentos. A percepção de regularidades é importante, mas ela não pode ser o MACETE para os cálculos e você se dar por convencido de que aprendeu o conteúdo. Aprenda mesmo o conteúdo!
Quadrado de números inteiros com dois ou mais algarismos terminados com o algarismo 5
Para números como descrito acima, calcular o quadrado possui um procedimento interessante:
1º) Suponha que o número analisado seja $K$;
2º) Retire o último algarismo de $K$ e eleve-o ao quadrado, no caso será sempre $5$, e seu quadrado $25$. Chamemos $Y = 25$;
3º) O restante dos algarismos formam um número $X$, multiplique esse número pelo número $X + 1$ (próximo número);
4º) O resultado do quadrado de $K$, será sempre os algarismos formados pela junção dos dois cálculos anteriores $[X \cdot (X + 1)$ e $Y]$.
Parece difícil não é mesmo! Mas vejamos que na prática é bem mais simples...
Números terminados com o algarismo $5$ e com no mínimo dois algarismos são $15, 25, 35, 45, 55, 65, 75, 85, 95, 105, 115, 125, 135, ..., 1005, 1015, ...$
Agora observe:
Você conseguiu compreender? Faça o teste para outros quadrados e confira!
E aí Pedro Rafael e demais leitores o que acharam do post? Ele começou com a ideia de algumas regrinhas básicas para encurtar procedimentos (existem várias outras regrinhas assim, quem sabe um outro post pra continuar...), mas no meio de tudo percebi algo que já venho falando há tempos com meus alunos, e surgiu um novo post (na verdade um Guest Post partilhado é um blog parceiro), que tal conferirem: Dicas que podem contribuir para a aprendizagem em Matemática.
Referências
[1] SALLA, Fernanda. Multiplicar por $10$, $100$ e $1.000$. REVISTA Nova Escola.[2] Contar (Matemática.com).











Comente este artigo: