O material que segue abaixo é um recorte de conteúdo e atividades que busca contemplar algumas habilidades de matemática para turmas de 6º ano. Este material também está disponível para download logo abaixo da imagem capa desta postagem.
Habilidades: Estabelecer relações entre números, expressas pelos termos é múltiplo de, é divisível por, é divisor de, é fator de. Classificar os números naturais em primos ou compostos.
Download
Seguem links para download do material organizado para algumas turmas de determinada escola. O cabeçalho está configurado para esta determinada escola, mas pode ser facilmente editado. O material está disponível para download e edição (.PDF e .docx) a partir de um dos dois links abaixo:
Múltiplos e divisores de um número natural
Múltiplos
Para saber se um número natural é múltiplo de outro número natural, basta efetuar a divisão entre eles. Exemplo:
Em uma divisão exata de números naturais (resto zero), temos que o dividendo é múltiplo do divisor e é múltiplo do quociente.
O menor múltiplo/submúltiplo de um número é $0$ (zero). Não existe um maior múltiplo de um número natural, pois o conjunto dos múltiplos de um número natural é infinito. Mais exemplos:
$M(3) = 0, 3, 6, 9, 12, 15, ...$
$M(5) = 0, 5, 10, 15, 20, 25, ...$
Divisores
Para saber se um número é divisor de outro basta verificar se ele é múltiplo deste outro número. Exemplo:
Veja que os divisores são aqueles que dividem o outro número e não deixam resto. Do exemplo acima, temos: $D(12) = 1, 2, 3, 4, 6, 12$. Algo importante de se observar é que tanto o divisor como o quociente são divisores do número natural (compare os números destacados em vermelho no exemplo, com os resultados dos cálculos. Os dois conjuntos são iguais).
O menor divisor de um número natural é o $1$. O maior divisor de um número natural é o próprio número. Mais exemplos:
$D(10) = 1, 2, 5, 10$.
$D(16) = 1, 2, 4, 8, 16$.
Número primo
Um número natural é primo quando é maior do que $1$ e tem apenas dois divisores naturais: o $1$ e ele mesmo. Por exemplo, o número $13$ é primo.
Como fazemos para reconhecer um número primo?
Dividimos o número pelos números primos $2$, $3$, $5$, $7$, $11$, $13$, $17$,..., até que o quociente seja menor ou igual ao divisor. Se a divisão não for exata para nenhum dos divisores, o número é primo.
Crivo de Eratóstenes
Um matemático do século 300 a.C. chamado Eratóstenes criou um método simples e prático para encontrar os números primos até um determinado valor. Acompanhe o professor no uso deste crivo.
Então, os números primos entre $1$ e $50$ são $2$, $3$, $5$, $7$, $11$, $13$, $17$, $19$, $23$, $29$, $31$, $37$, $41$, $43$ e $47$.

Número composto
Caso o número seja maior do que $1$ e não seja primo, o chamaremos de composto, então, um número composto é aquele que possui mais que dois divisores. Por exemplo, $9$ é um número composto, pois $D(9) = 1, 3, 9$.
Na imagem acima, observe que em azul estão os números compostos maiores que $1$ e menores ou igual a $50$. Os números compostos de $1$ a $50$ são: $4$, $6$, $8$, $9$, $10$, $12$, $14$, $15$, $16$, $18$, $20$, $21$, $22$, $24$, $25$, $26$, $27$, $28$, $30$, $32$, $33$, $34$, $35$, $36$, $38$, $39$, $40$, $42$, $44$, $45$, $46$, $48$, $49$, $50$.
Tarefa
1. Encontre os 5 primeiros múltiplos de cada número natural abaixo:
a) $ M(7)$ ______, ______, ______, ______, ______.
b) $ M(14)$ ______, ______, ______, ______, ______.
c) $ M(16)$ ______, ______, ______, ______, ______.
d) $ M(17)$ ______, ______, ______, ______, ______.
e) $ M(18)$ ______, ______, ______, ______, ______.
f) $ M(20)$ ______, ______, ______, ______, ______.
g) $ M(22)$ ______, ______, ______, ______, ______.
2. Determine os divisores dos números abaixo:
a) $ D(3)$ _______________________________________.
b) $ D(6)$ _______________________________________.
c) $ D(8)$ _______________________________________.
d) $ D(12)$ ______________________________________.
e) $ D(13)$ ______________________________________.
f) $ D(14)$ _______________________________________.
g) $ D(15)$ ______________________________________.
h) $ D(20)$ ______________________________________.
i) $ D(25)$ _______________________________________.
j) $ D(36)$ _______________________________________.
3. Quantos divisores possui um número primo?
4. Qual é o único número primo par?
5. Um número composto é um número que tem:
a) nenhum divisor.
b) apenas um divisor.
c) exatamente dois divisores.
d) um ou dois divisores.
e) mais de dois divisores.
6. Qual é o menor número primo ímpar?
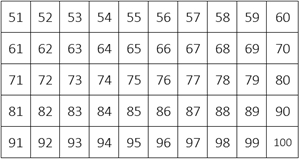
7. Use o crivo de Eratóstenes e encontre os números primos entre $50$ e $100$:
8. Marque V (verdadeiro) ou F (falso) para as afirmações:
a) ______ O número $1$ é primo.
b) ______ O único número primo par é o zero.
c) ______ Todos os números primos são ímpares.
d) ______ Existe um único número primo par.
e) ______ O maior número primo com dois algarismos é o $97$.
9. Escreva os números compostos entre $1$ e $100$.
Outras recomendações sobre este tema aqui no blog




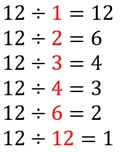




Comente este artigo: