Um exercício que pode ser observado por vários raciocínios são os desafios com representações figurais (objetos geométricos e outras figuras diversas) que já são moda nas redes sociais faz um bom tempo. Retomamos um dos desafios encontrados no Facebook para discutir sobre algumas formas de se pensar e apresentar uma solução, algo muito importante na matemática e que tem deixado de lado. Os recursos computacionais são importantes nos processos de ensino e de aprendizagem, mas não podemos priorizar o seu uso.
Não aprendemos de fato a matemática ou damos por esquecidos procedimentos por falta de prática quando tornamo-nos dependentes, por exemplo, de uma calculadora ou de um outro recurso computacional, quando não acabamos tapeados pela falta de entendimento do problema que nos é apresentado ou pelo uso incorreto de determinado recurso. O esforço mental é importante para o bem estar.
O desafio
Neste desafio, observe valores em linhas e em colunas que sugerem somas das formas geométricas e cada uma delas com um valor específico. Vamos apresentar alguns procedimentos para chegar à resposta deste desafio. A intenção é incentivar diferentes formas de pensar e lidar sobre o mesmo problema e ainda, de transitar entre diferentes áreas da matemática.
Dois raciocínios lógicos
- Muito simples:
É intuitivo pensar que somando os valores em cada linha obtemos os resultados apresentados, o mesmo ocorre para as colunas, então um raciocínio muito simples, e é a ideia que acredito ser fundamental é o pensamento de que se somarmos todos os valores na horizontal o resultado deve ser o mesmo que todos os valores na vertical; assim, procedemos $11+12+12+?=13+9+12+15$, o que nos fornece que o valor da soma na última linha é $14$.
- Clássico por apreciação:
Por apreciação procedemos observando o que é evidente, e vamos seguindo alguns passos, como se estivéssemos resolvendo um sistema de equações de forma algébrica (claro que alguns procedimentos podem ser diferentes, dependendo do observador, mas o resultado prevalece).
- Na linha 2, temos quatro quadrados resultando $12$, então concluímos por cada quadrado vale $3$.
- Na linha 3, temos que dois losangos e dois círculos resultam $12$, então concluímos que um losango somado a um círculo vale $6$.
- Na coluna 1, temos por reorganização um quadrado adicionado à soma de um losango com um círculo, adicionados de outro losango resultando $13$, mas quadrado igual a $3$ e losango com um círculo igual a $6$, então temos $9$ mais um losango igual a 13, o que resulta em um losango vale $4$.
- Na coluna 2, se um quadrado vale $3$, então temos três círculos mais $3$ igual a $9$, o que resulta que um círculo vale $2$. Mais simples ainda, se losango vale $4$ e losango mais círculo valem $6$, então círculo vale $2$.
- Na linha 1, se o círculo vale $2$, então temos $3 \cdot 2$ mais triângulo igual a $11$, o que resulta que o triângulo vale $5$.
- Pronto. Um losango mais um círculo mais um quadrado mais um triângulo valem $4+2+3+5=14$.
Uma sugestão de resposta usando a álgebra
Tomando que o círculo seja $x$, o triângulo seja $y$, o quadrado seja $z$ e o losango seja $t$, podemos organizar a representação na figura acima em dois grupos (sistemas) de equações:
- Na horizontal
$ \begin{cases} x+x+x+y=11 \\ z+z+z+z=12 \\ t+x+t+x=12 \\ t+x+y+z=? \end{cases}$
- Na vertical
$ \begin{cases} x+z+t+t=13 \\ x+z+x+x=9 \\ x+z+t+z=12 \\ y+z+x+y=15 \end{cases} $
Resolvemos por inúmeros procedimentos, um deles é seguindo o procedimento de apreciação já indicado acima.
- $4 \cdot z=12 \Rightarrow z=3$.
- $2 \cdot t + 2 \cdot x = 12 \Rightarrow t + x = 6$.
- $z + (x + t) + t = 13 \Rightarrow 3 + 6 + t = 13 \Rightarrow t = 4$.
- $x + z + x + x = 9 \Rightarrow 3 \cdot x + 3 = 9 \Rightarrow x = 2$ ou mais simples, do segundo e terceiro procedimentos $t + x = 6 \Rightarrow 4 + x = 6 \Rightarrow x = 2$.
- $x + x + x + y = 11 \Rightarrow 3 \cdot 2 + y = 11 \Rightarrow y = 5$.
- $t+x+z+y= 4 + 2 + 3 + 5 = 14$.
Lançaremos novamente este desafio nas redes sociais. Havendo algum outro procedimento, o transcreveremos aqui.
Estamos no Telegram em t.me/ticnamatematica.


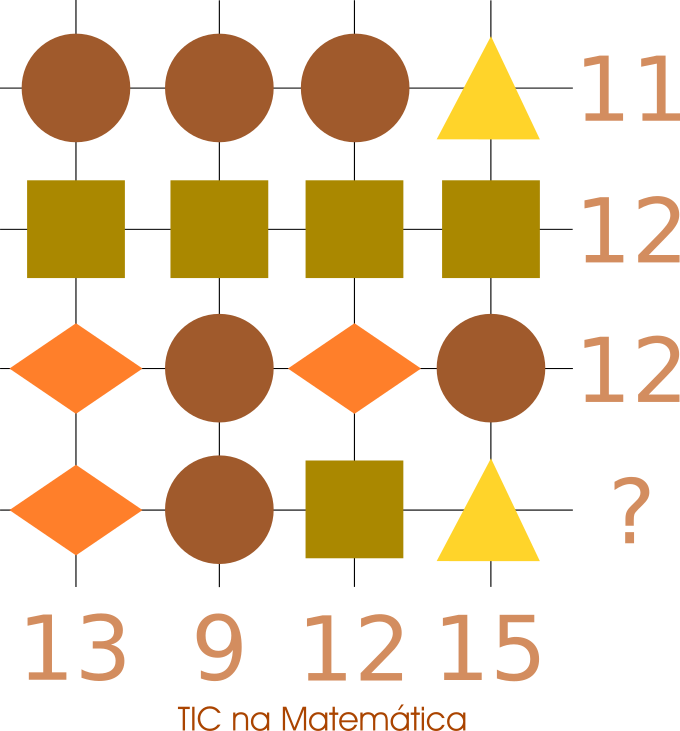

Comente este artigo: